八一八赌博中的数学应用（2）
（二） 凯利公式
这次我们以一个赌局开场：
有一个简单的2赔1的赌局，扔硬币下注。规则如下：硬币扔出正面则赢2元，如果扔出来反面则输1元，初始本多为100元，每一次押注都可以投入任意金额。如何下注能达到最高的收益呢？
虽然在赌场老板的眼中，赌场的只有两种人：穷人和未来的穷人。但是不可否认，赌徒通常分为两种，1种是冒险主义者；另外一种则是保守主义者。
针对于这个赌局，极端的冒险主义者的玩法是：要玩就玩票大的，一次性押注100，幸运的话，一次正面就可以获利200元，但如果输了，那么就是100元的资产拱手让人。总之，输赢的比例都是50%对50%，也没什么好遗憾的，刺激！
对于极端的保守主义者，他们的想法就是谨慎点，每次都是投注一块钱，慢慢来。正面可以赢两块钱，反面就是输一块钱。但是人不可能没有贪念，玩了20把之后突然发现，别人一次下注10块钱就可以赢20，而自己一次只有两块，得保证10把不输的情况下才能赢20。看上去，太过于保守也不好，玩着玩着总会觉得心痛，正如过年抢红包的那样，好像自己错过了几个亿！
这个问题看似无解，毕竟扔硬币嘛，50%的概率会扔出正面，50%的概率扔出反面。幸运女神眷顾的话，怎么都是赢；手气背的话也不能怨天尤人。100块一次性投注太多了，1块钱一块钱的投，又太少，我们到底应该怎么做呢？
赌场上的普通老哥，估计随心情而赌，下注时默念阿弥陀佛，财神爷保佑；但数学家则会告诉你，最佳的投注金额应是本多的25%，即第一次投注25元。
先让我们来拜见一下这位将数学原理纯熟地应用在赌场中，大杀四方以至于被赌场禁入的数学天才爱德华·索普先生（Edeard Thorp）。
索普大神在赌场中大杀四方的神器就是我们下面要介绍的凯利公式。
其实最早，科学家翰·拉里·凯利（John L. Kelly,Jr.）在1956年推导出凯利公式的初衷是为了帮助信息大神香农来解决信息传送问题，虽然他是以赛马为模型，推导出这个神奇的公式。
其中，
表示应每次投注额占本金的比例；
表示获胜的概率（在扔硬币赌局中，即为抛出硬币正面的概率）;
表示失败的概率， 
;
表示赔率， =盈利/本金，例如，付出1元的本金，如果赢了，总共收入3元，其中2元是盈利，1元是返还的本金，则赔率为2， =2/1=2
在这个公式中， 分子 
表示赢面，我们专业点，用数学术语来说就是对于单位本金时盈利的期望值。此外，这个公式仅适用于失败时投入的本金全部赔光光这种情况。
凯利公式并没有像凯利先生想的那样，解决通讯中的信号传送问题，却成功的引起了另一位爱好21点游戏的同事，也就是我们索普大神的兴趣。经过索普大神的深入研究，还在各个赌场之间得到验证，尤其在着名的赌城拉斯维加斯，索普大神一战成名，由于赢钱太多，从此大神被赌场拉入了黑名单……
言归正传，凯利公式告诉我们，要选择最佳投注比，才能长期获得最高盈利。
在这个例子中，硬币抛出的正反面的概率都是50%，所以和，也就是获胜和失败的概率都是50%，而赔率=盈利/本金=2（赢了2元）/1（本金1元）=2，所以 
=（2×0.5-0.5）/2=0.25.
这就是我们的结论，手持100元本金，第一次，应拿出资金的25%，也就是25块钱来进行下注，如果赢了手里的钱变成150元，输了就变成75元；第二次，仍然拿出手里全部资金的25%进行下注918博天堂真人游戏，即37.5或18.75元。就这样一次次的赌下去，直到最后赢的次数达到总次数的50%，你就实现了赌局收益的最大化。
为什么呢？
设初始本金为 
，每次下注比例为 
。第一次投入资金为 
，若赢得赌注，收益率为 
，手里资金变为：剩余本金+投入本金+收益，即 
；若输了，损失率为 
，则最终资金为 
，赌场中，大多数情况是赌注全部输掉，此时为100%，只要你不加杠杆，损失率一般不会超过100%的，即最多是损失掉你投入的资金，不会有额外的损失。
如果一个人赌了 
次，其中赢了 
次，输了 
次，则手里的资金变为： 
设 
是 次赌博游戏的平均收益率，则：
另赌博赢的概率为 
，输的概率为 
，上式简化为 
我们的目的就是找到平均收益率 取得最大值时，下注比例的最佳取值。简要数学推导过程如下：
上面包含和的公式适用性更广，可以用于投资理财、炒股；包含赔率 的公式仅适用于输了就要赔掉全部本金的赌博。
最佳投注比例公式（凯利公式）有如下特点：
- 最佳投注比例与初始本金
无关； - 最佳投注比例与多次赌博过程中输、赢的顺序无关，重要的是总共赢了几次、输了几次；
- 只有玩的次数足够多，凯利公式才能发挥作用，即实际赢的概率接近 。
- 只有 时，即期望收益为正时才有赢的可能，否则长期玩下去必输无疑。下图给出了不同赔率和获胜概率时的最佳下注比例。
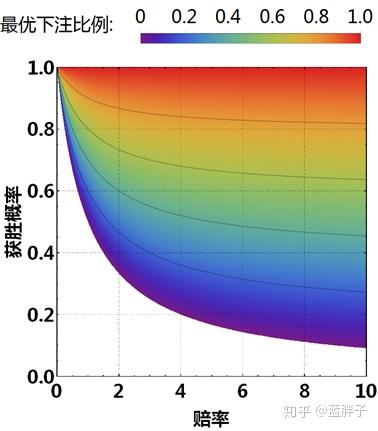
时，即期望收益为正时才有赢的可能，否则长期玩下去必输无疑。下图给出了不同赔率和获胜概率时的最佳下注比例。
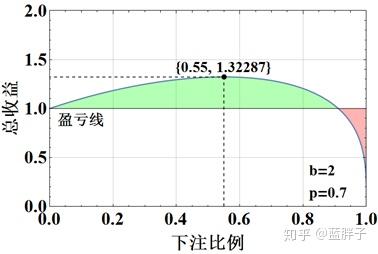
下图给出了赔率为2，获胜概率为0.7时，总收益与下注比例之间的关系。利用凯利公式，下注比例为55%时，收益最高，图中的曲线也给出了相同的结论。注意，下注比例过高，是会亏损的噢~
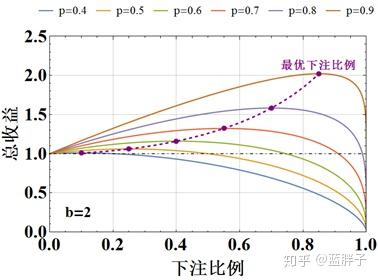
下图是赔率固定为2，获胜概率不同时，总收益与下注比例之间的关系。图中紫色虚线给出了不同情况下的最优下注比例。
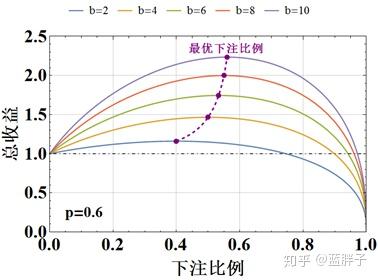
下图是获胜概率固定为0.6918.com博天堂，赔率不同时，总收益与下注比例之间的关系。图中紫色虚线给出了不同情况下的最优下注比例。
后记：
允许我在碎碎念几句，您问我这世界上有赌神么，有，还真的有那么为数不多的几位“赌神”，比如信息论的发明者香农博士，数学家爱德华·索普大神，路径理论的创始人蒙特卡洛等等。他们通过一系列复杂的计算和坚实的数学理论，把某些赌博游戏的赢率扳回到50%以上，也仅仅是50%以上。比如赌21点，可以依靠强大的头脑去算牌，提高赢牌的概率。但老实说，就凭咱们这帮读书时上课打瞌睡，现在连求导积分都不记得的普通人来说，还是先老老实实地读完以下三条准则，不是让您赌博，而是三条投资的建议：
- 期望值 为0时，赌局为公平游戏，这时不应该下任何赌注；
- 期望值 为负时，庄家占优势，这时更不应该下任何赌注；
- 期望值 为博彩游戏正时，可以按照凯利公式投注赚钱，这时风险最小。
为0时，赌局为公平游戏，这时不应该下任何赌注；还是那句话，真爱生命，远离赌博，尤其当你面对的都是大数学家们几个世纪总结出来的下注规律，而自己除了默念财神爷保佑却没有别的门道时，即便是有幸运女神眷顾，我们也无法和凯利公式抗衡，毕竟人都是有贪念的，见好就收在普通赌徒中不可能存在的，继续赌下去，博彩游戏总有一天会输掉一切。
